Como se preparar para as questões de Geometria em um teste de matemática
Informações gerais
Geometria é apenas um nome extravagante para o estudo de linhas e formas. Existem certamente princípios e tópicos adicionais difíceis, mas temos aqui o básico. Você precisará dominá-los antes de abordar conceitos mais avançados.
(Note que se uma figura for rotulada como “exemplo” neste guia, ela pode não ser a única representação dessa figura, mas é uma delas.)
Pontos e Linhas
Um ponto em geometria é um local. Ele não tem comprimento, largura ou profundidade. Usamos um ponto e uma letra maiúscula para mostrar um ponto.
Um segmento de linha é definido por dois pontos e todos os pontos entre eles. Os dois pontos são chamados de pontos finais do segmento. Um segmento tem uma dimensão: o comprimento. Para escrever um segmento, coloque uma barra sobre os dois pontos finais. \Este segmento:

Uma linha se estende em ambas as direções sem fim. Para escrever uma linha, coloque uma barra com duas setas sobre quaisquer dois pontos da linha. \A linha:

Um raio começa em um ponto final e se estende sem fim em apenas uma direção. Para escrever um raio, coloque uma barra com uma seta apontando para a direita sobre dois pontos: o ponto final e qualquer outro ponto (nessa direção). \O raio:

Nota: você não pode escrever um raio com a seta apontando para a esquerda como se estivesse sobre a seta para a esquerda. Além disso, a ordem é importante. \Não é a mesma coisa que a seta para a direita. A primeira letra é sempre o ponto de partida de um raio.
Duas linhas, segmentos ou raios são perpendiculares se formarem um ângulo recto (ver abaixo). Use o símbolo {\perp} para denotar perpendicularidade. Por exemplo, se a perpendicularidade é perpendicular à perpendicularidade, você pode escrever {AB} {CD} {CD}.
Exemplos: 
Duas linhas são paralelas se nunca se cruzarem. Se a seta para a direita esquerda (AB) estiver paralela à seta para a direita (CD), pode escrever a seta para a esquerda para a direita (AB) em paralelo com a seta para a direita (CD).
Exemplos: 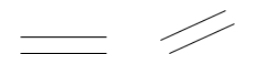
Formas de plano
Em geometria, um plano é uma superfície bidimensional plana que se estende infinitamente longe. As duas dimensões são comprimento e largura. Assim, formas planas são formas “planas”, como quadrados, círculos e triângulos.
Formas Comuns
Um polígono é uma superfície fechada sobre um plano delimitado por segmentos de linha chamados de lados.
Exemplos: 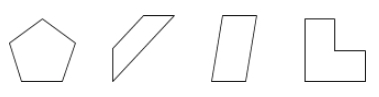
Um polígono regular é um polígono em que todos os segmentos e ângulos interiores são congruentes.
Exemplos:
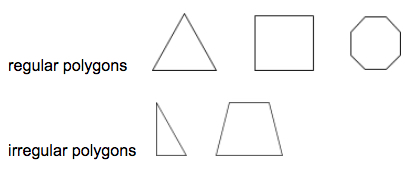
Um triângulo é um polígono de três lados.
Exemplos:
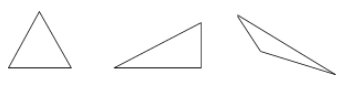
Quadrilaterais – polígonos de quatro lados
Um paralelogramo é um tipo de quadrilátero onde lados opostos são paralelos e congruentes. Os ângulos opostos de um paralelogramo também são congruentes.
Exemplos: 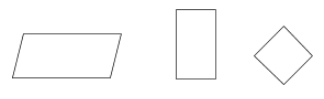
Um rectângulo é um paralelogramo com quatro ângulos rectos.
Exemplos: 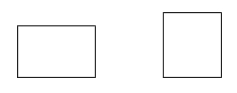
Um losango é um paralelogramo em que todos os quatro lados são congruentes.
Exemplos: 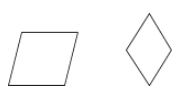
Um quadrado é um paralelogramo que é ao mesmo tempo um losango e um rectângulo (todos os lados são congruentes e todos os ângulos são rectos).
Exemplos: 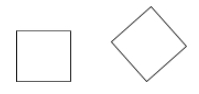
Um trapézio é um quadrilátero com apenas um par de lados paralelos.
Exemplos: 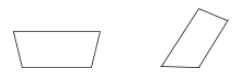
Polígonos com mais de quatro lados
(^1\) Um polígono com 11 lados também pode ser chamado de endecagon ou undecagon.
Medindo Formas
O perímetro é a distância total em torno de um polígono. Para encontrar o perímetro, basta somar os comprimentos de todos os lados. Se o polígono for regular (todos os lados são congruentes) e o comprimento de um lado for de um lado, então multiplique o número de lados por um para encontrar o perímetro. Por exemplo, o perímetro de um pentágono regular é P_text{reg pentagono}=5s}